随着金融市场的日益发展和复杂化，期权模型的应用逐渐成为金融领域的重要工具，期权模型不仅能够为投资者提供风险管理的手段，还能为企业决策层提供有效的决策支持，本文将探讨期权模型的应用场景、原理及其在金融市场中的实际运用。

期权模型的基本原理

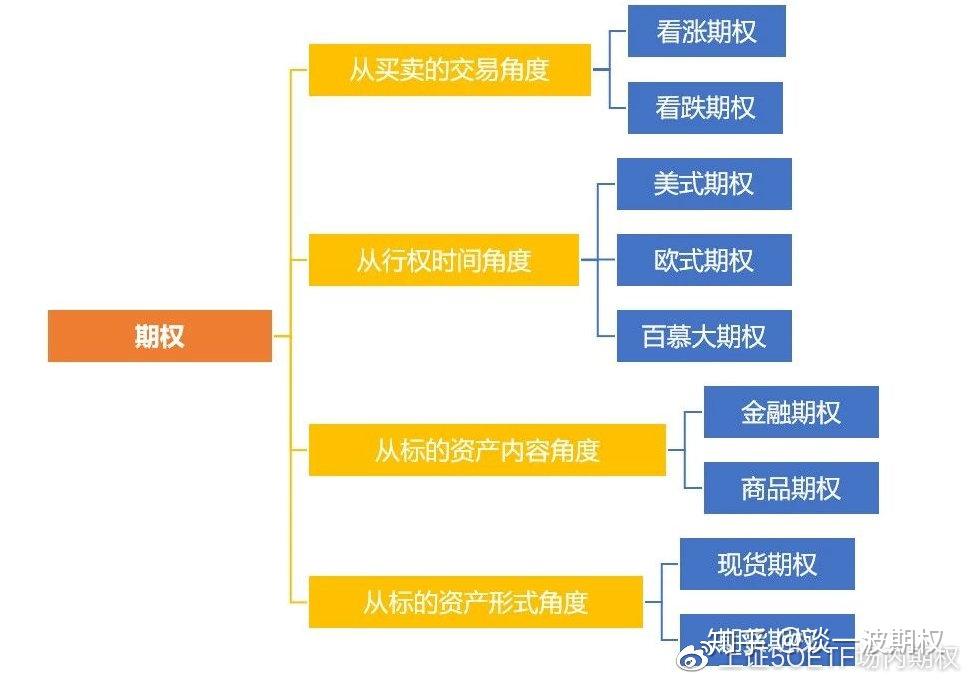
期权是一种金融衍生品，它给予持有者在未来某一特定日期以特定价格购买或出售基础资产的权利，期权模型则是通过数学和统计学方法，对期权价格、风险及收益进行量化分析的工具，期权定价模型，如二叉树模型、Black-Scholes模型等，为投资者提供了评估期权价值的有效方法。

期权模型的应用场景

1、风险管理

期权模型在风险管理领域具有广泛应用，企业可以通过购买期权来规避未来现金流风险，如原材料采购风险、产品销售风险等，投资者可以利用期权模型评估投资组合的风险敞口，从而制定相应的风险管理策略。

2、投资策略

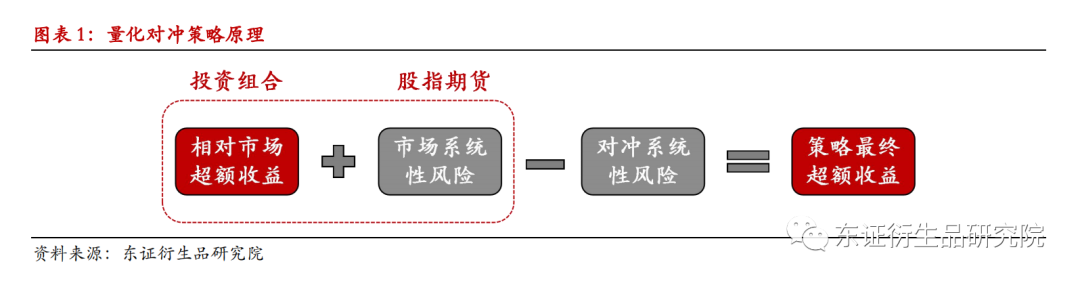
期权模型在投资策略制定中发挥着关键作用，投资者可以通过构建包含期权的投资组合来实现收益最大化，同时控制风险，利用期权模型进行股票对冲、套利交易等。

3、企业决策支持

期权模型还可用于企业决策支持，企业可以通过分析期权价值来评估潜在的投资项目、并购活动以及资本结构决策等，这有助于企业做出更加明智的决策，从而提高企业的竞争力。

期权模型的实际应用

1、金融市场监管

在金融市场监管领域，期权模型被广泛应用于评估金融机构的风险敞口和资本充足率，监管机构可以利用期权模型来评估金融机构的稳健性，从而制定相应的监管政策。

2、金融产品创新

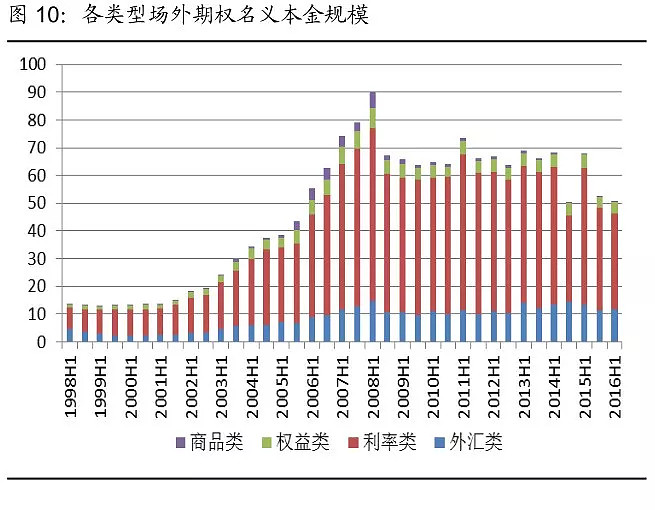
随着金融市场的不断创新，期权模型在金融产品创新中发挥着重要作用，金融机构可以利用期权模型设计出更加复杂的金融衍生品，如奇异期权、障碍期权等，这些创新产品为投资者提供了更多的投资选择，丰富了金融市场。

3、企业财务管理

在企业财务管理领域，期权模型被广泛应用于企业投资决策、资本结构决策以及风险管理等方面，企业可以利用期权模型评估潜在项目的价值，从而做出更加明智的投资决策，企业还可以通过购买期权来管理汇率风险和商品价格风险，从而确保企业的稳健运营。

不同期权模型的比较分析

1、二叉树模型与Black-Scholes模型

二叉树模型和Black-Scholes模型是两种常用的期权定价模型，二叉树模型适用于离散时间下的期权定价，而Black-Scholes模型则适用于连续时间下的期权定价，在实际应用中，两种模型各有优劣，投资者需根据具体情况选择合适的模型。

2、其他期权模型的探讨

除了二叉树模型和Black-Scholes模型外，还有其他一些期权定价模型，如蒙特卡洛模拟、有限差分法等，这些模型在特定情况下也具有应用价值，如蒙特卡洛模拟在路径依赖型期权的定价中具有较高的准确性。

期权模型作为金融衍生品市场的关键工具，在风险管理、投资策略、企业决策支持等领域具有广泛应用，随着金融市场的不断创新和发展，期权模型的应用将更加广泛，投资者和企业应加强对期权模型的研究和应用，以提高决策效率和风险管理水平。